Aerodynamics in racing
Aerodynamics is the science that studies objects moving through air. It is closely related to fluid dynamics as air is considered a compressible fluid. Nowadays, aerodynamics is the utmost important factor in Formula One car performance. It has even nearly become one of the only aspects of performance gain due to the very marginal gains that can currently be made by engine changes or other mechanic component development. This downforce can be likened to a virtual increase in weight, pressing the car down onto the road and increasing the available frictional force between the car and the road, therefore enabling higher cornering speeds.
Furthermore, as Formula One teams have the greatest resources to develop aero efficiency of its cars, the greatest strives are made here. F1 teams have unrivalled CFD computing power and at least one full time wing tunnel, only for validating and improving their designs.
While basic aerodynamic methods and formulas can be simply resolved, other properties are verifiable with empirical formulas. More complex shapes such as airplanes or racing cars are however impossible to calculate precisely, rendering computational fluid dynamic systems (CFD applications on super computers) and wind tunnels an absolute requirement to validate designs.
Application in Formula One
F1 (and in general, all winged racing cars) can be considered to be canard configurations in the sense that the front and back wings are on opposite sides of the centre of gravity and both are "lifting" (strongly) in the same direction, in this case creating downforce.
From a spectator's point of view, a car can be considered in (at least) 3 parts: the front wing, the car's body and the rear wing. Each of the parts can be optimised for the required downforce at a minimum of drag. Practically however, every component has its influence on the behaviour of the car and cannot be regarded as an individual component. As a result, no element is tested individually, but always a complete scale model of a car.
Because a complete racing car is a very complex system, teams of engineers usually evolve the car step by step, developing a particular item and check its effect on the car. Such overall effect can then be calculated with Amdahl's law:
Here is the fraction of the system (when this fraction generates 5% of the car's drag, then
is 0.05) that can be improved,
is the improvement factor on this fraction (division of the drag in Newtons and the new drag force after improving that element), and
is the overall improvement that will be achieved.
After verifying its improvement, the car's efficiency is determined and then simulated on different tracks to see on where it is useful. That usefulness is always the
result of a reduction in drag or an increase in downforce.
Drag
Drag is the aerodynamic force that is opposite to the velocity of an object moving through air (or any other fluid). Its size is proportional to the speed differential between the air and the solid object. It is therefore unimportant if either the air is moving around a static object or if the object is moving at a speed through static air.
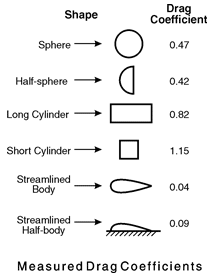Drag comes in various forms, one of them being friction drag which is the result of the friction of the solid molecules against air molecules in their neighbourhood. Friction and its drag depend on both the fluid and the solid properties. A smooth surface of the solid for example produces less skin friction compared to a rough one. For the fluid, the friction varies along with its viscosity and the relative magnitude of the viscous forces to the motion of the flow, expressed as the Reynolds number. Along the solid surface, a boundary layer of low energy flow is generated and the magnitude of the skin friction depends on conditions in the boundary layer.
Additionally, drag is a form of resistance from the air against the solid moving object. This form of drag is dependent on the particular shape of a wing, and is therefore called form drag. As air flows around a body, the local velocity and pressure are changed, effectively creating a force.
Interference drag or induced drag on the other hand is the result of vortices that are generated behind the solid object. Due to the change of direction of air around the wing, a vortex is created where the airflow meets unchanged, straight flow. The size of the vortex, and thereby its drag strength increases with an increasing angle of attack of the aerofoil. As a primary source of possible drag reduction, Formula One teams try to counteract this drag by adding end plates to wings or with fillets at the suspension arms.
Other sources of drag include wave drag and ram drag. The first is unimportant for normal racecars as it occurs when the moving object speeds up to the speed of sound. Ram drag on the other hand is the result of slowing down the free airstream, as in an air inlet.
The amount of drag that a certain object generates in an airflow is quantified in a drag coëfficient. This coëfficient expresses the ratio of the drag force to the force produced by the dynamic pressure times the area. Therefore, a of 1 denotes that all air flowing onto the object will be stopped, while a theoretical 0 is a perfectly clean air stream.
At relatively high speeds, ie. at high Reynolds number (), the aerodynamic drag force can be calculated by this formula:
where is the force of drag (in Newton),
the density of the air,
the speed of the object relative to the fluid (in m/s),
the reference surface and
the coëfficient of drag. Note the minus sign and the vector
which indicate that the resulting drag force is opposite to the movement of the object.
Downforce
Aerofoils in motorsports are often called wings, referring to aircraft wings. In fact they are very similar. F1 wings and winglets aim to generate high downforce, by having a high angle of attack, thus also increasing the drag of the aerofoil.
The evolution of aerofoils to what they are now is mainly thanks to the genious and research of a few well known scientists. In 1686, Sir Isaac Newton presented his three laws of motion, one of them being the conservation of energy. He stated that energy is constant in a closed system, although it can be converted from one type to another. Out of that theory, Daniel Bernouilli deducted a formula proving that the total energy in a steadily flowing fluid system is a constant along the flow path. An increase in the fluid’s speed must therefore be matched by a decrease in its pressure. Adding up the pressure variation times the area around the entire body determines the aerodynamic force on the body.
An aerofoil's operation can be easily explained when you consider a wing in a steady, laminar flow of air. As air is a gas, its molecules are free to move around and may have a different speed at different locations in the airstream. As downforce generating aerofoils are mostly designed with more thickness on the lower side, the lower airstream is slightly reduced in surface, hence increasing the flow speed and decreasing the pressure. On top of the wing, the airspeed is lower, and thus the pressure difference will generate a downward force on the wing. Additionally, and in line with Newton's third law of motion, downforce wings are never straight and induce a new turning of the airflow. More specifically, the shape of the wing will turn air upwards and change its velocity. Such speed creates a net force on the body.
This shows that a force causes a change in velocity
, or also, a change in velocity generates a force. Note that a velocity is a vectorial unit, having a speed and a direction component. So, to change of either of these components, you must impose a force. And if either the speed or the direction of a flow is changed, a force is generated.
It is very important to note that the turning of the fluid occurs because the molecules of the fluid stay in contact with the solid body since the molecules are free to move. Any part of the solid body can deflect a flow. Parts facing the oncoming flow are said to be windward, and parts facing away from the flow are said to be leeward. Both windward and leeward parts deflect a flow. Ignoring the leeward deflection leads to the incorrect "skipping stone" theory of lift.
You can simulate airflow around a simple aerofoil with NASA's Foilsim toolkit.
Downforce is however often explained by the "equal transit time" or "longer path" theory, stating that particles that split ahead of the aerofoil will join together behind it. In reality however, the speed difference of air particles above and below a wing is much larger than what is expected with this theory.
While these simplified versions are the basics of lift and downforce generation, the reality can hardly be simplified and is a complex study, requiring high power computer systems. For a gas, we have to simultaneously conserve the mass, momentum, and energy in the flow. Hence, a change in the velocity of a gas in one direction results in a change in the velocity of the gas in a direction perpendicular to the original change. The simultaneous conservation of mass, momentum, and energy of a fluid (while neglecting the effects of air viscosity) are called the Euler Equations after Leonard Euler. Several computer algorithms are based on these equations to make an approximation of the real situation.
Because of the complexity, today's Formula One cars are designed with CFD (computational fluid dynamics) and CAD (computer aided design) that allows engineers to design a car, and immediately simulate the airflow around it, incorporating environmental parameters like traction, wind speed and direction, and much more.
